In Arphy’s walk to school, we tracked the distance he walked and the time it took him to get to his destination.
Watch the next clip and think about the ways in which his journey is described.
The clip shows information about the length of the track (distance in metres) and the time taken (in seconds).
If we know the distance and the time, we can calculate how fast he was moving. This is called speed.
Speed is a property of moving bodies. It is symbolised by the letter v.
At uniform motion it is calculated as the ratio of the distance s, to the time, t, taken for object to travel that distance.
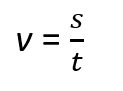
The unit for speed is
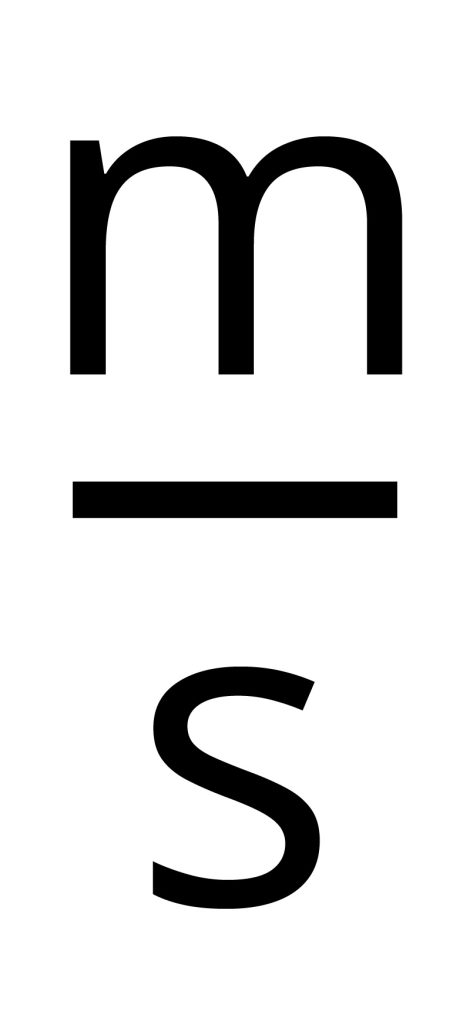
Imagine that Arphy has left the house and you want to catch up with him. You need to know not only how fast he went, but also in which direction. This is because velocity is a vector quantity and therefore has both magnitude and direction. Here, we will solve simplified situations where we only need to know the length of the trajectory – the track and the time. Then we calculate the average speed, which is a scalar quantity and has only magnitude. Both velocity and speed are denoted by the same letter v, the difference is that the vector quantity is denoted by the “bold” letter v, and in our “scalar examples” we denote the speed only by a simple v
Because of the simplicity of the examples, we will focus only on speed.
See an example:
Jan’s house is 1200 metres away from the school. He usually walks this distance in 15 minutes (which is 900 seconds). What is his average walking speed?
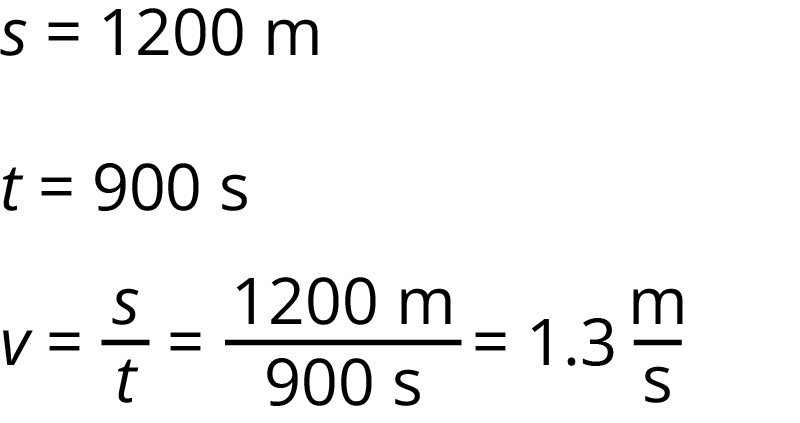
Jan walked at an average speed of 1.3 m/s
TASK 1
Maja’s house is 1800 metres away from the school. She usually walks this distance in 20 minutes. What was her average walking speed?
First, convert minutes into the corresponding unit (seconds).
Mark the correct answer:
a) 1.5 m/s
In transport, we usually talk about longer distances between places (given in kilometres) and longer journey times (given in hours). Therefore, we usually give speed in units (kilometres per hour).
Examples can be found in road signs, e.g. what is the speed limit in a residential area. In a car, on a bicycle, on a smartwatch, the speed of movement is displayed in km/h.
Conversion is
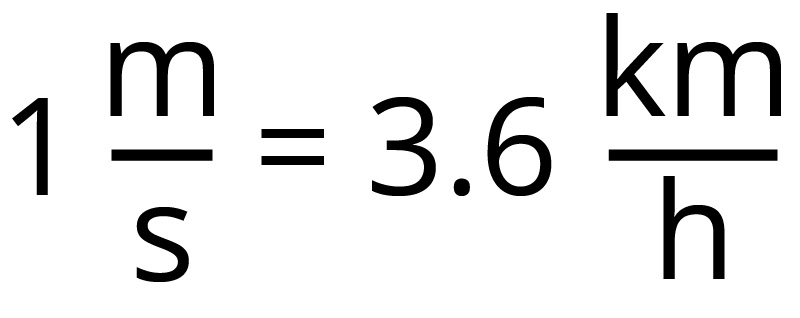
The speed limit for vehicles around the school is 30 km/h.

30 km/h = 8.3 m/s
How fast did Usain Bolt, the fastest man on Earth, run when he set the world record for the 100 m? Would he have exceeded the speed limit around the school?

How would you check the answer?
The runner completed the 100 m in 9.58 seconds. Dividing the distance by the time, we find that his speed was 10.4 m/s.
To get an idea of his average speed, let’s convert it to km/h. Multiply the result by 3.6.
His speed was 37.6 km/h.
Usain Bolt would have exceeded the speed limit around the school.
Task 2
The Novak family went to visit their grandmother. It’s a 140-kilometre journey to their grandmother’s house. It took them 2 hours to complete the journey.
What was their average speed?
Mark the correct answer:

The Novak family drove at an average speed of 70 km/h.
Task 3
The Murn family went on a trip. It is a 210 km long journey to the destination. It took them 3 hours to complete the journey. What was the average speed of their journey? Put it in m/s.
Mark the correct answer:
a) 19.4 m/s


