Depending on the speed, the motion can be uniform or non-uniform.
In everyday life, we often encounter movements where the speed of bodies changes over time.
When the speed of an observed body increases, this is called accelerated motion.
When the speed of the observed body decreases, this is called decelerated motion.
If the speed of the observed body does not change during the motion, it is called uniform motion.
Example 1
See the two videos below.
The first one shows a car moving linear uniformly. It means that the path is linear, and the speed does not change as it moves.
The second shot shows the car in linear accelerated motion. It means that the paths is linear and the speed uniformly increases with time.
Acceleration is constant.
Task 1:
Sort the examples below into the appropriate categories.
Acceleration is the quotient of the change in velocity and the time over which the speed has changed. It is denoted by the lower case letter a.
To calculate the acceleration, we need data about the speed of the body at time t1 and at time t2.
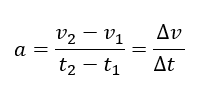
When the speed increases or decreases uniformly, we speak of uniformly accelerating or uniformly decelerating motion.
In uniformly accelerating motion, the speed varies in direct proportion to time. The coefficient of proportionality is the acceleration-
Δv = a ⋅ Δt
Acceleration is the quotient of the change in speed and the time over which the speed has changed. It is denoted by the lower case letter a.
To calculate the acceleration, we need data about the speed of the body at time t1 and at time t2.
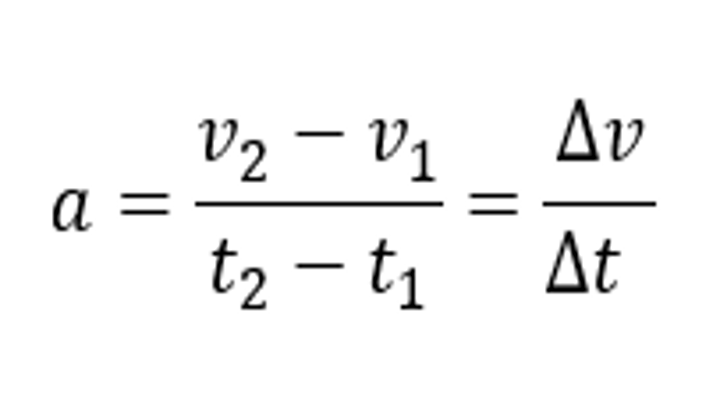
When the speed increases or decreases uniformly, we speak of uniformly accelerating or uniformly decelerating motion.
In uniformly accelerating motion, the speed varies in direct proportion to time. The coefficient of proportionality is the acceleration.
Δv = a ⋅ Δt


